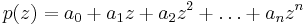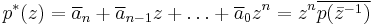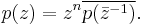Reciprocal polynomial

In mathematics, for a polynomial p with complex coefficients,

$p(z) = a_0 %2B a_1z %2B a_2z^2 %2B \ldots %2B a_nz^n \,\!$

we define the reciprocal polynomial, p*

$p^*(z) = \overline{a}_n %2B \overline{a}_{n-1}z %2B \ldots %2B \overline{a}_0z^n = z^n\overline{p(\bar{z}^{-1})}$

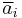where $\overline{a}_i$ denotes the complex conjugate of $a_i \,\!$ .

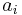A polynomial is called self-reciprocal if 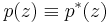$p(z) \equiv p^{*}(z)$ .

If the coefficients a_i are real then this reduces to a_i = a_n−i. In this case p is also called a palindromic polynomial.

If p(z) is the minimal polynomial of z₀ with |z₀| = 1, and p(z) has real coefficients, then p(z) is self-reciprocal. This follows because

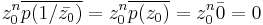$z_0^n\overline{p(1/\bar{z_0})} = z_0^n\overline{p(z_0)} = z_0^n\bar{0} = 0$ .

So z₀ is a root of the polynomial 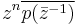$z^n\overline{p(\bar{z}^{-1})}$ which has degree n. But, the minimal polynomial is unique, hence

$p(z) = z^n\overline{p(\bar{z}^{-1})}.$

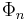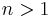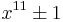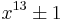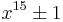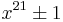A consequence is that the cyclotomic polynomials $\Phi_n$ are self-reciprocal for $n > 1$ ; this is used in the special number field sieve to allow numbers of the form $x^{11} \pm 1$ , $x^{13} \pm 1$ , $x^{15} \pm 1$ and $x^{21} \pm 1$ to be factored taking advantage of the algebraic factors by using polynomials of degree 5, 6, 4 and 6 respectively - note that $\phi$ of the exponents are 10, 12, 8 and 12.

References

External links

Reciprocal Polynomial (on MathWorld)

Reciprocal polynomial

See also

References

External links